5. Entscheidbare und erkennbare Sprachen

Das Modell Turing-Maschine

Um zu präzisieren, was es bedeutet, dass ein mathematisches Problem berechenbar ist, stellte ALAN TURING 1936 die später nach ihm benannte Turing-Maschine vor, die die Einzelschritte nachbildet, die ein Mensch beim Rechnen auf dem Papier ausführt. Es gibt andere Präzisierungsvorschläge, die aber alle äquivalent zur Turing-Maschine sind.

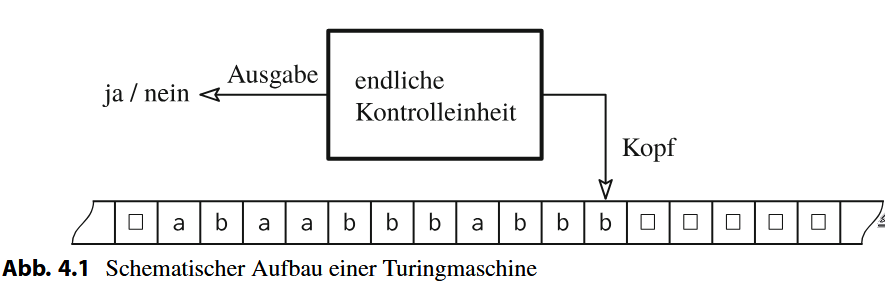
Eine Turingmaschine ist ein abstraktes Berechnungsmodell, welches aus zwei Teilen besteht. Zum einen besitzt eine Turingmaschine einen Speicher. Bei diesem handelt es sich um ein unbeschränktes Band, welches aus einer Folge von Zellen besteht. In den Zellen können bestimmte Zeichen stehen. Zugriff hat man jedoch immer nur auf eine Position des Bandes, und zwar auf die Zelle, an welcher der Kopf des Bandes steht. Die Zelle an dieser Stelle kann man beschreiben oder auslesen. Auf alle anderen Zellen hat man (vorerst) keinen Zugriff. Man kann jedoch den Kopf des Bandes bewegen. Dabei hat man die Möglichkeit, den Kopf um eine Position nach links oder nach rechts zu verschieben. Neben dem Speicher besitzt eine Turingmaschine auch einen Steuermechanismus, manchmal auch als endliche Kontrolleinheit bezeichnet. Er legt fest, wie der Kopf bewegt wird und welche Zeichen auf das Band geschrieben werden. Der Steuermechanismus hat in etwa die Funktionalität eines endlichen Automaten. Das heißt, er besitzt endlich viele Zustände. Während der Ausführung befindet man sich immer in einem Zustand, und das Programm legt die Zustandsübergänge fest. Hier bezeichnen wir als Konfiguration das Tupel aus Zustand, Bandinhalt und Kopfposition. Das eigentliche Programm definiert nun die möglichen Übergänge zwischen den Konfigurationen.

Definition:

• Q (Zustandsmenge): Eine endliche, nicht-leere Menge von Zuständen, in denen sich die Maschine befinden kann.

• Σ (Eingabealphabet): Eine endliche Menge von Symbolen, aus denen das Eingabewort besteht, das auf dem Band steht. Das Eingabealphabet ist immer eine Teilmenge des Bandalphabets (Σ ⊆ Γ). Das sind die Zeichen, die bei der Startkonfigurtion bereits auf dem Band stehen, z.B:

• Γ (Bandalphabet): Eine endliche Menge aller Symbole, die auf dem Band gelesen und geschrieben werden können. Wichtig ist, dass das Blank-Symbol (□) immer Teil des Bandalphabets ist, aber nie Teil des Eingabealphabets.

• δ (Überführungsfunktion): δ: Q × Γ → Q × Γ × {L, R, N}

Q × Γ × {L, R, N} ist ein Tripel, das die Aktion der Maschine beschreibt: Der neue Zustand, in den die Maschine wechselt, das neue Symbol, das auf das Band an die aktuelle Position beschrieben wird (es kann auch das alte Symbol sein), die Bewegung des Kopfes: L (links), R (rechts) oder N (neutral, stehen bleiben).

• q₀ (Anfangszustand): Der Zustand, in dem die Maschine ihre Arbeit beginnt.

• □ (Blank-Symbol): Ein spezielles Symbol, das eine leere Zelle auf dem ansonsten unendlichen Band darstellt (□ ∈ Γ, □ ∉ Σ).

Eine Berechnung einer Turingmaschine ist eine Folge von Konfigurationen C1, C2...,Ck so dass

• C1 = q0 (die Folge beginnt in der Startkonfiguration)
• Ci geht über in Ci+1 für alle i = 1,...,k-1

Falls Ck akzeptierend --> akzeptierende Berechnungn, sonst verwerwende Berechnung Falls Ck weder akz noch verw ist -> heißt die Folge nicht-haltend

Eine Sprache L heißt Turing-erkennbar, rekursiv aufzählbar, oder semi-entscheidbar, wenn es eine TM gibt welche sie erkennt.

"Erkennbar" (und nicht mehr nur "akzeptierend"), weil TM im Vergleich zu den weniger mächtigere Automaten neben "Akzeptieren" und "Verwerfen" auch "Nicht-Halten" kann. Nicht akzeptieren kann auch heißen, dass die Maschine endlos weiter läuft.

Erkennen heißt dass alle w in der Sprache sind, die Eigenschaft haben, dass die Maschinen auf ihnen übergeht in einen akzeptierenden Zustand.

Eine Sprache heißt Turing-entscheidbar, rekursiv, oder der Länge nach aufzählbar, wenn es eine TM M gibt, welche sie entscheidet. Die TM Mheißt dann Entscheider für L(M).

tipp

Jede Turing-entscheidbare Sprache ist Turing-erkennbar. Aber nicht jede erkennbare Sprache ist entscheidbar. Entscheiden ist mehr als Erkennen!

Nicht-Deterministische Turing-Maschinen (NTMs)

Die Übergangsfunktion von Nicht-deterministische Turing-Maschinen ist die Potenzmenge aus Zustand, Bandalphabet und Kopfbewegung.

Berechenbarkeit

Was bedeutet berechenbar? Alles was ein Mensch oder ein Computer (nach Anweisungen) berechnen kann. Wie können wir den Begriff "berechenbar" formalisieren?

Bei einer Berechnung haben wir immer eine Eingabe und eine Ausgabe. Das Problem "ist n eine Primzahl?" ist berechnebar. Wir geben eine Zahl n ein, und erhalten eine Ausgabe wahr oder falsch zurück. Das heißt, dieses Problem ist berechenbar: Die Funktion liefert eine Ausgabe hält an und gelangt nicht in eine endlose Schleife.

Eine partielle Funktion ist eine Funktion, die nicht für jede erdenkliche Eingabe definiert ist (bei bestimmten Eingaben liefert sie keine Ausgabe).

Stopp-Konfiguration (u, q, f(...) □ v): Die Maschine muss in einen Zustand gelangen, wobei u und v irgendwelche Wörter aus dem Bandalphabet sind (sie sind das Ergebnis von Zwischenberechnungen).

Beispiel: Nehmen wir eine Additionsfunktion add(3, 2). Die Eingabe w₁="111" und w₂="11" würde auf dem Band so aussehen (der Pfeil ^ zeigt die Lesekopfposition):

... □ 1 1 1 □ 1 1 □ ...

^

Nachdem die Additions-Maschine fertig ist, könnte das Band so aussehen:

... □ b b b □ 1 1 1 1 1 □ ...

Hier wäre u="b b b", das Ergebnis f(3,2) ist 11111, und v ist leer. Das ist ein gültiges Ergebnis.

Die charakteristische Funktion

Beim Wortproblem geht es darum, zu entscheiden, ob ein Wort wzu einer Sprache L gehört. Wenn das Wortproblem einer Sprache entscheidbar ist, dann sagt man auch, dass die Sprache entscheidbar ist.

Ein Problem kann man formal als eine Funktion verstehen. Diese Funktion bildet eine Menge von Eingaben (den Problemfäälen) auf eine Menge von Lösungen ab.

f: Eingaben --> Lösungen

Ein Entscheidungsproblem ist ein Problem, bei dem die Antwort entweder "ja" oder "nein" lautet. **Die Funktion für ein Entscheidungsproblem bildet demnach alle möglichen Eingabewörter (Σ*) auf {0, 1} ab.

Genau diese Art von Funktion, die nur 1 (Ja) oder 0 (Nein) als Ergebnis hat, nennt man die charakteristische Funktion einer Menge oder Sprache A.

Definition: Charakteristische Funktion

Eine Turingmaschine, die ein Entscheidungsproblem löst, hat genau eine Aufgabe: Sie berechnet die charakteristische Funktion der zugehörigen Sprache. Für jede gegebene Eingabe x ermittelt sie, ob die Antwort 1 oder 0 ist.

Turing-entscheidbar

Eine Sprache L ⊆ Σ∗ ist (Turing-)entscheidbar, wenn es eine Turing-Maschine T gibt, die die charakteristische Funktion χL der Sprache L berechnet. Die Turing-Maschine T entscheidet die Sprache L.Der Funktionswert ε der charakteristischen Funktion χL wird durch das Zeichen □ im Arbeitsfeld dargestellt.

Church-Turing-These

Die intuitive berechenbaren Funktionen sind genau die Funktionen, die eine Turing-Maschine berechnen kann. Alle vernünftigen Berechnungsmodelle (Javaprogramme, Registermaschine usw.) sind gleichmächtig zu einer Turing-Maschine.

Deshalb postulierte der Logiker ALONZO CHURCH 1936 die nach ihm benannte Churchsche These, dass mit der Turing-Berechenbarkeit genau die Berechenbarkeit im intuitiven Sinne beschrieben wird. Beweisbar ist diese These natürlich nicht, dazu müsste dann wieder präzisiert werden, was denn “berechenbar im intuitiven Sinne“ ist!

Das Halteproblem

Warum ist das Halteproblem interessant?

Wenn wir ein Programm schreiben, erwarten wir, dass dieses irgendwann anhält. Manchmal passiert das aber nicht; Das Programm läuft und läuft, gefangen in einer Endlosschleife, vielleicht wegen eines Fehlers in einer while-Schleife. Es wäre daher sehr hilfreich, ein Werkzeug zu haben, das jedes beliebige Programm im Voraus überprüfen und uns sagen kann, ob es jemals anhalten wird oder nicht.

Genau diese Frage behandelt das Halteproblem aus der theoretischen Informatik. Es fragt: Kann man einen Algorithmus schreiben, der für jedes beliebige Programm P und jede beliebige Eingabe E nach endlicher Zeit entscheiden kann, ob P mit der Eingabe E irgendwann anhält oder für immer weiterläuft?

Die Idee eines "Haltealgorithmus"

Die Idee ist, einen universellen "Haltealgorithmus" zu entwickeln. Dieser Algorithmus würde zwei Dinge als Eingabe erhalten:

• Ein Programm P (z. B. als Quellcode)
• Eine Eingabe E für dieses Programm P

Das Ergebnis des Haltealgorithmus sollte sein:

• "Ja", falls das Programm P mit der Eingabe E nach endlicher Zeit zum Stehen kommt.
• "Nein", falls das Programm P mit der Eingabe E in eine Endlosschleife gerät.

Der entscheidende Punkt ist, dass dieser Haltealgorithmus selbst immer anhalten und eine definitive Antwort geben muss, auch und gerade dann, wenn das zu prüfende Programm P niemals anhalten würde.

Einen solchen universellen Haltealgorithmus kann es nicht geben. Das Halteproblem ist unentscheidbar.

Warum ist das Halteproblem unentscheidbar? Der Widerspruchsbeweis

Um zu beweisen, dass etwas unmöglich ist, verwendet man oft einen Widerspruchsbeweis. Die Logik ist wie folgt:

• Annahme: Wir nehmen an, es gäbe einen funktionierenden Haltealgorithmus. Nennen wir ihn H.
• Konstruktion: Wir bauen ein neues Programm, das wir U (für "unmöglich") nennen.
• Widerspruch: Wir zeigen, dass das Programm U zu einem logischen Widerspruch führt, weshalb unsere ursprüngliche Annahme (dass H existiert) falsch sein muss.

Das unmögliche Programm "U"

Dieses Programm U ist so konstruiert:

• U nimmt als Eingabe den Quellcode eines Programms, nennen wir es P --> (U(P)).
• Im Inneren von U wird unser angenommener Haltealgorithmus H aufgerufen. U stellt H eine sehr spezifische Frage: "Wird das Programm P anhalten, wenn es sich selbst als Eingabe bekommt?" --> (H(P, P))
• Jetzt kommt der entscheidende Punkt des Widerspruchsbeweises: U ist so programmiert, dass es das genaue Gegenteil von dem tut, was H vorhersagt:

Wenn H sagt: "Ja, P wird mit der Eingabe P anhalten", dann geht U absichtlich in eine Endlosschleife. Wenn H sagt: "Nein, P wird mit der Eingabe P niemals anhalten", dann hält U sofort an.

Der Widerspruch

Bisher ist U nur ein theoretisches Programm. Da es einen Quellcode hat, können wir nun eine paradoxe Frage stellen: Was passiert, wenn wir U mit seinem eigenen Quellcode als Eingabe füttern? Also, was macht U(U)?

Das sind die beiden möglichen Fälle:

• Fall 1: Der Haltealgorithmus H sagt voraus, dass U(U) anhalten wird.

Gemäß der Definition von U muss es in diesem Fall in eine Endlosschleife gehen.

Das bedeutet, U(U) hält nicht an.

Widerspruch! Die Vorhersage von H war falsch.

• Fall 2: Der Haltealgorithmus H sagt voraus, dass U(U) nicht anhalten wird (also in einer Endlosschleife läuft).

Gemäß der Definition von U muss es in diesem Fall sofort anhalten.

Das bedeutet, U(U) hält an.

Widerspruch! Auch hier war die Vorhersage von H falsch.

In beiden Fällen liefert der Haltealgorithmus H für die Eingabe U(U) eine falsche Antwort. Ein Algorithmus, der nicht für alle Eingaben funktioniert, ist aber kein universeller Lösungsalgorithmus. Daraus folgt, dass unsere ursprüngliche Annahme falsch war. Es kann keinen universellen Haltealgorithmus geben.

Das Postsche Korrespondenzproblem (PKP)

Ein weiteres unentscheidbares Problem ist das Postsche Korrespondenzproblem (kurz PKP). Die Eingabe einer PKP-Instanz besteht aus einer Folge von Paare von Wörtern, die wir als Dominotypen bezeichnen. Eine Sequenz heißt Dominoset.

Beim PKP-Problem fragen wir, ob wir aus den Dominotypen eine Reihe bilden können, sodass die obere und untere Zeile das gleiche Wort bilden. Die Wörter ergeben sich aus der Konkatenation der gegebenen Teilwörtern.

Gegeben sei ein Dominoset S1 = ((ab, a), (ba, bb), (b, abb))

Eine Lösung könnte so aussehen:

Definition:

Kontrollfragen

1. Was ist der Hauptunterschied zwischen einer Turing-erkennbaren und einer Turing-entscheidbaren Sprache?
2. Welche der folgenden Komponenten ist in der formalen Definition einer Turing-Maschine T=(Q,Σ,Γ,δ,q0​,□,F) nicht explizit enthalten?
3. Was besagt die die Church-Turing-These?
4. Was ist die zentrale Idee hinter dem Widerspruchsbeweis für die Unentscheidbarkeit des Halteproblems?
5. Gegeben sei eine Instanz des Postschen Korrespondenzproblems (PKP). Was ist eine gültige 'Lösung'?
6. Bei der Definition der Berechenbarkeit einer Funktion f durch eine Turing-Maschine, was bedeutet die Stopp-Konfiguration (u,q,f(w1​,...,wn​)□v)?
7. Was ist der wesentliche Unterschied in der Überführungsfunktion einer nicht-deterministischen Turing-Maschine (NTM) im Vergleich zu einer deterministischen (DTM)?
8. Warum ist das Blank-Symbol (□) nicht Teil des Eingabealphabets (Σ)?

Übungen

1. Turing-Maschine entwerfen: Beschreibe formell (als 7-Tupel) und mit einer Übergangstabelle eine Turing-Maschine, die die Sprache L=anbncn∣n≥1 entscheidet. Erkläre die Strategie deiner Maschine in Worten.

2. Konfigurationsfolge: Gegeben sei eine einfache Turing-Maschine, die jedes 'a' auf dem Band durch ein 'b' ersetzt und dann stoppt. Die Überführungsfunktion ist: δ(q0​,a)=(q0​,b,R) und δ(q0​,□)=(qf​,□,N). Gib die vollständige Folge von Konfigurationen für die Eingabe aa an.

Entscheidbarkeit vs. Erkennbarkeit: Erkläre mit eigenen Worten, warum die Sprache des Halteproblems (LTM​) zwar Turing-erkennbar, aber nicht Turing-entscheidbar ist. Warum kann eine Maschine die "Ja"-Fälle erkennen, aber nicht immer eine "Nein"-Antwort garantieren?

Charakteristische Funktion: Definiere die charakteristische Funktion χL​ für die Sprache L aller Wörter über dem Alphabet Σ=0,1, die mit '0' beginnen und mit '1' enden. Gib die Funktionswerte für die Wörter 0101, 1010, 0 und ε (leeres Wort) an.

Church-Turing-These anwenden: Ein Kommilitone behauptet, er habe einen neuen Quantencomputer entworfen, der Probleme lösen kann, die für Turing-Maschinen unentscheidbar sind. Wie würdest du unter Berufung auf die Church-Turing-These argumentieren, dass dies (höchstwahrscheinlich) nicht der Fall ist?

Beweisidee Halteproblem: Fasse die Kernaussagen des Widerspruchsbeweises für die Unentscheidbarkeit des Halteproblems in 3-4 Sätzen zusammen. Fokussiere dich dabei auf die Konstruktion der "paradoxen" Maschine.

PKP-Instanz lösen: Finde eine Lösung für die folgende PKP-Instanz oder begründe, warum es keine gibt: S = ((1, 101), (10, 00), (011, 11))

Berechenbarkeit einer Funktion: Beschreibe auf einer konzeptionellen Ebene, wie eine Turing-Maschine die Funktion f(w)=wR (die Umkehrung eines Wortes w) berechnen könnte. Wie würde die Start- und eine mögliche Stopp-Konfiguration für die Eingabe abc aussehen?

Reduktion erklären: Das Konzept der Reduktion ist zentral, um die Unentscheidbarkeit von Problemen zu beweisen. Erkläre das Prinzip "Problem A ist auf Problem B reduzierbar" am Beispiel des Halteproblems und des PKP.

Grenzen der Modelle: Ordne die folgenden Sprachklassen ihrer maximalen Mächtigkeit nach und nenne das jeweils zugehörige Automatenmodell: reguläre Sprachen, kontextfreie Sprachen, Turing-entscheidbare Sprachen, Turing-erkennbare Sprachen.

Lösungen

1. Für eine entscheidbare Sprache hält die Turing-Maschine immer an; für eine erkennbare Sprache nur für Wörter, die in der Sprache sind. Ein Entscheider muss für jede Eingabe halten, ein Erkenner nur für die Wörter, die er akzeptiert.
2. Die Kopfposition ist Teil der Konfiguration einer Turing-Maschine, aber nicht Teil ihrer festen, formalen Definition.
3. Die Klasse der von Turing-Maschinen berechenbaren Funktionen entspricht genau der Klasse der intuitiv berechenbaren Funktionen. Die These schlägt eine Brücke zwischen einem formalen Modell und einem intuitiven Konzept.
4. Man nimmt an, es gäbe einen Halte-Entscheider und wendet ihn auf eine speziell konstruierte Maschine an, die das Gegenteil von dessen Vorhersage tut.
5. Eine Folge von Indizes (mit Wiederholungen), sodass die Konkatenation der oberen Wörter gleich der Konkatenation der unteren Wörter ist.
6. Das Ergebnis der Funktion muss auf dem Band stehen, umgeben von beliebigem 'Rechenmüll'. Die Wörter u und v repräsentieren genau diesen 'Rechenmüll', der vor und nach dem eigentlichen Ergebnis stehen darf.
7. Das Ergebnis der Überführungsfunktion einer NTM ist eine Menge von möglichen Übergängen. Dies ist der entscheidende Punkt. Eine NTM kann für eine gegebene Konfiguration mehrere mögliche Folgekonfigurationen haben, was durch die Potenzmenge ausgedrückt wird.,
8. Um das Ende der ursprünglichen Eingabe eindeutig vom unbeschriebenen Teil des Bandes zu unterscheiden. Die Eingabe ist ein endliches Wort auf einem unendlichen, mit Blanks gefüllten Band. Das Blank-Symbol markiert die Grenze.